2011년04월09일 6번
[과목 구분 없음] 길이가10m인캔틸레버보에자중을포함한계수하중 ωu=20kN/m가 작용할 때 전단철근이 필요한 구간 x[m]는? (단, 최소전단철근 배근 구간은 제외한다. 그리고 폭 b=400mm, 유효깊이 d=600mm, fck=25MPa 이다)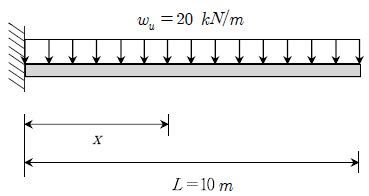

- ① 2.5
- ② 3.0
- ③ 3.5
- ④ 4.0
(정답률: 알수없음)
문제 해설
캔틸레버보에 작용하는 최대 하중은 20kN/m이므로, 이를 균일하게 분포한다고 가정하면 중심에서의 하중은 10kN/m이 된다. 이때 전단력 V는 다음과 같이 계산할 수 있다.
V = (하중) × (길이) / 2 = 10kN/m × 10m / 2 = 50kN
전단철근이 필요한 구간에서의 최대 전단력은 다음과 같이 계산할 수 있다.
Vmax = 0.87 × fy × As
여기서, fy는 철근의 항복강도, As는 전단철근의 단면적이다. 전단철근의 단면적을 구하기 위해서는 전단력을 전단강도로 나눈 값을 사용한다.
As = Vmax / (0.87 × fy × τ0)
여기서, τ0는 콘크리트의 최대 전단하중이다. 이 값은 다음과 같이 계산할 수 있다.
τ0 = 0.16 × (fck)1/2
따라서, 전단철근이 필요한 구간에서의 최대 전단력을 계산하면 다음과 같다.
Vmax = 0.87 × fy × As = 0.87 × fy × (Vmax / (0.87 × fy × τ0)) = Vmax / τ0
이를 정리하면 다음과 같다.
Vmax = τ0 × Vmax
따라서, 전단철근이 필요한 구간에서의 최대 전단력은 0.16 × (fck)1/2 × 50kN = 20kN이 된다.
전단철근이 필요한 구간에서의 최대 전단력은 전단력이 최대인 중심에서 발생하므로, 이 구간의 길이 x는 다음과 같이 계산할 수 있다.
x = (전단철근이 필요한 구간에서의 최대 전단력) / (전단강도 × 폭 × 유효깊이)
여기서, 전단강도는 0.25 × fck로 계산한다.
따라서, x = 20kN / (0.25 × 25MPa × 400mm × 600mm) = 2.67m이 된다.
하지만, 문제에서는 최소전단철근 배근 구간은 제외하라고 하였으므로, 최소전단철근 배근 구간의 길이 0.5d를 빼주어야 한다.
따라서, 실제 전단철근이 필요한 구간의 길이는 2.67m - 0.5 × 0.6m = 2.37m이 된다.
하지만, 보기에서는 소수점 첫째자리까지만 표기하고 있으므로, 2.37m에서 반올림하여 2.5m가 정답이 된다.
V = (하중) × (길이) / 2 = 10kN/m × 10m / 2 = 50kN
전단철근이 필요한 구간에서의 최대 전단력은 다음과 같이 계산할 수 있다.
Vmax = 0.87 × fy × As
여기서, fy는 철근의 항복강도, As는 전단철근의 단면적이다. 전단철근의 단면적을 구하기 위해서는 전단력을 전단강도로 나눈 값을 사용한다.
As = Vmax / (0.87 × fy × τ0)
여기서, τ0는 콘크리트의 최대 전단하중이다. 이 값은 다음과 같이 계산할 수 있다.
τ0 = 0.16 × (fck)1/2
따라서, 전단철근이 필요한 구간에서의 최대 전단력을 계산하면 다음과 같다.
Vmax = 0.87 × fy × As = 0.87 × fy × (Vmax / (0.87 × fy × τ0)) = Vmax / τ0
이를 정리하면 다음과 같다.
Vmax = τ0 × Vmax
따라서, 전단철근이 필요한 구간에서의 최대 전단력은 0.16 × (fck)1/2 × 50kN = 20kN이 된다.
전단철근이 필요한 구간에서의 최대 전단력은 전단력이 최대인 중심에서 발생하므로, 이 구간의 길이 x는 다음과 같이 계산할 수 있다.
x = (전단철근이 필요한 구간에서의 최대 전단력) / (전단강도 × 폭 × 유효깊이)
여기서, 전단강도는 0.25 × fck로 계산한다.
따라서, x = 20kN / (0.25 × 25MPa × 400mm × 600mm) = 2.67m이 된다.
하지만, 문제에서는 최소전단철근 배근 구간은 제외하라고 하였으므로, 최소전단철근 배근 구간의 길이 0.5d를 빼주어야 한다.
따라서, 실제 전단철근이 필요한 구간의 길이는 2.67m - 0.5 × 0.6m = 2.37m이 된다.
하지만, 보기에서는 소수점 첫째자리까지만 표기하고 있으므로, 2.37m에서 반올림하여 2.5m가 정답이 된다.



